Für ihre herausragenden Leistungen zeichnete das TopMath-Board Dominik Schmid (Lehrstuhl für Wahrscheinlichkeitstheorie) und Claudia Stadlmayr (Lehr- und Forschungseinheit Algebra) ex aequo mit dem TopMath Award 2020 aus.
Der TopMath Award ist eine Auszeichnung für Promovierende des Programms, die sich durch herausragende Forschungsleistungen besonders hervorgetan haben. Er wird einmal jährlich verliehen. Nach einem Vorschlag ihrer Mentorin, ihres Mentors oder des Fachstudienberaters werden die Kandidat*innen zum Ende des Sommersemesters zu einer Eigenbewerbung aufgefordert. Jeweils in seiner letzten Jahressitzung bestimmt das TopMath-Board nach ausführlicher Beratung den*die Preisträger*in. Der TopMath Award ist mit 500 € dotiert und wird im feierlichen Rahmen der Absolventenfeier der Fakultät für Mathematik der TUM vergeben.
Preisträger des TopMath Award 2020 sind ex aequo Dominik Schmid (Lehrstuhl für Wahrscheinlichkeitstheorie) und Claudia Stadlmayr (Lehr- und Forschungseinheit Algebra).
Dominik Schmid hielt 2019/20 etliche Vorträge vor internationalem Fachpublikum, reiste zu Forschungszwecken an renommierte Universitäten und verfasste vier Beiträge, die im Rahmen internationaler Kooperationen entstanden, etwa mit Evita Nestoridi (Princeton University) oder Nicos Georgiou (University of Sussex). Ausgezeichnet wurde er für einen Beitrag, den er gemeinsam mit Nina Gantert (TUM) und Evita Nestoridi zum Ausschlussprozess mit offenen Rändern verfasste.
Auch für Claudia Stadlmayr war 2019/20 ein sehr erfolgreiches Jahr. Ihre bisherigen Forschungen resultierten in zwei Beiträgen, von denen sie einen in Kooperation mit Gebhard Martin (Universität Bonn), einen als alleinige Autorin verfasste. Das rege Interesse der internationalen Fachwelt an ihrer Arbeit zeigte sich an Einladungen zu Forschungsaufenthalten und Vorträgen auf internationalen Konferenzen. Mit dem TopMath Award 2020 würdigte das TopMath-Board sie für eben diese Leistungen, die in ihrem Fachbereich in diesem frühen Karrierestadium höchst ungewöhnlich sind.
Wir gratulieren den Preisträgern herzlich und wünschen Ihnen weiterhin viel Erfolg bei der Verfolgung ihrer mathematischen Ziele!
Dominik Schmid: Mischungszeiten für Ausschlussprozesse
Text: Dominik Schmid
In einer gemeinsamen Forschungsarbeit mit Nina Gantert und Evita Nestoridi untersuche ich den Ausschlussprozess mit offenen Rändern. Dabei handelt es sich um ein interagierendes Teilchensystem, mit dem beispielsweise das Verhalten von Gasen oder die Bildung von Staus modelliert werden kann.
Vereinfacht gesagt nehmen wir in diesem Modell an, dass wir Teilchen auf einem eindimensionalen, endlichen Gitter platzieren, wobei jede Position nur durch maximal ein Teilchen gleichzeitig besetzt sein darf. Die Teilchen bewegen sich nun zufällig zu benachbarten Gitterplätzen, wobei ein neuer Platz nur dann eingenommen werden kann, wenn das Ziel nicht bereits durch ein anderes Teilchen besetzt ist. Zusätzlich erlauben wir, dass Teilchen mit einer gewissen Wahrscheinlichkeit an den Endpunkten das Gitter verlassen und neue Teilchen entstehen können.
Unser Ziel ist es, die Zeit zu analysieren, die benötigt wird, bis sich von jeder möglichen Ausgangskonfiguration von Teilchen ausgehend ein (zufälliges) Gleichgewicht im System eingestellt hat. Dies lässt sich durch sogenannte Mischungszeiten erzielen. Abhängig von den Übergangswahrscheinlichkeiten der Teilchen im Gitter sowie den Wahrscheinlichkeiten an den Endpunkten können wir verschiedene Phasen mit unterschiedlichem Mischungsverhalten identifizieren. Darüber hinaus können wir in einigen Fällen das sogenannte „Cutoff-Phänomen“, einen scharfen Übergang in der Konvergenz zum Gleichgewicht, nachweisen.
Link zur Arbeit: "Mixing times for the simple exclusion process with open boundaries"
Siehe auch die Simulationen auf der persönlichen Homepage
Claudia Stadlmayr: Symmetrien und Singularitäten auf del Pezzo Flächen
Text: Claudia Stadlmayr
Eine besondere Klasse glatter, projektiver Flächen stellen die sogenannten "del Pezzo Flächen" dar, welche sich, nach ihrem erstmaligen Studium durch ihren Namensgeber Pasquale del Pezzo (1887), in den vergangenen gut hundert Jahren als fundamentale Objekte in der algebraischen Geometrie und als Grundbausteine in der Klassifikation algebraischer Varietäten herausstellten. Indem wir das klassische Studium der Symmetriegruppen solcher Flächen mit dem modernen Standpunkt der Automorphismenschemata zusammenbrachten, konnten Gebhard Martin und ich in einer gemeinsamen Arbeit die Klassifikation schwacher del Pezzo Flächen mit globalen Vektorfeldern über Körpern beliebiger Charakteristik erreichen.
Link zur Arbeit: "Weak del Pezzo surfaces with global vector fields" (with G. Martin)
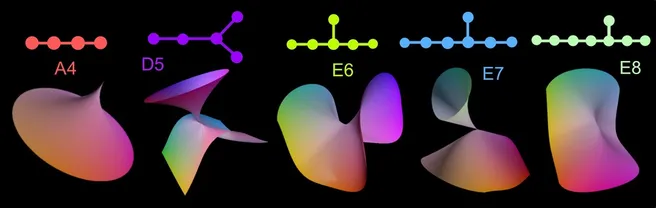
Indem man die Anforderung, glatt zu sein, verwirft und stattdessen milde Singularitäten, sogenannte "rationale Doppelpunkte", erlaubt, lässt sich der Begriff der del Pezzo Flächen auch auf singuläre projektive Flächen ausweiten. Solche Flächensingularitäten können (abhängig von ihrem assoziierten Dynkin-Diagramm) in verschiedene Typen eingeteilt werden. In meiner zweiten Arbeit gelang es, eine weitere klassische Frage (1934 eröffnet von Patrick Du Val), nämlich welche Typen solcher Singularitäten auf del Pezzo Flächen auftreten, abschließend für beliebige Charakteristiken, Grade und Picardränge zu beantworten.
Link zur Arbeit: "Which rational double points occur on del Pezzo surfaces?"
Rationale Doppelpunkte vom Typ A4, D5, E6, E7 und E8 mit ihren assoziierten Dynkin-Diagrammen
Erfreulicherweise trafen beide dieser Arbeiten auf Interesse in der Fachwelt, was mir die Gelegenheit gab, über letztgenannte im Moskauer Iskovskikh-Seminar online vorzutragen und die Resultate der Arbeit zu schwachen del Pezzo Flächen im "Zoom-Algebraische-Geometrie Marathon" vorzustellen. Die Idee dieses originellen Formats war es, jede der 24 Stunden des "Tags des Wissens" mit einem Vortrag zur algebraischen Geometrie zu begehen -- die Standorte der Vortragenden quer über alle Zeitzonen verteilt. Es war für mich eine große Ehre mit diesem, meinem ersten Konferenzvortrag als jüngste und einzige noch nicht promovierte Vortragende für unsere mitteleuropäische Zeitzone anzutreten.
Siehe auch den Bericht "Claudia Stadlmayr beim ZAG-Marathon"
Letztendlich, nachdem meine geplanten zwei Forschungsaufenthalte von je zwei Monaten in Moskau am Steklov Institut und in Salt Lake City an der University of Utah im vergangenen Jahr pandemiebedingt leider nicht stattfinden konnten, bin ich sehr dankbar für die fruchtbare Kollaboration auf virtuellem Wege und die Gelegenheit durch Online-Vorträge immer mehr in die Fachwelt der algebraischen Geometrie hineingewachsen zu sein.
Stimmen zu den Preisträgern und ihren Leistungen
"Dominik Schmid is interested in discrete probability theory, in particular interacting particle systems, mixing times for Markov chains and stochastic processes in random media. Several of his contributions have been internationally recognized and the topics have been taken up by well-known probabilists. His PhD thesis is based on five papers, the common theme being exclusion processes. In his new preprint
'Mixing times for the TASEP in the maximal current phase', not included in the PhD thesis, he solves a general conjecture for the particular case of Totally Asymmetric Exclusion Process (TASEP).
He has also contributed to different topics as random walks on trees and self-similar fragmentations.
Dominik Schmid has won a DAAD PRIME fellowship for the project 'Analytic and geometric properties of exclusion processes' and he will move to Princeton University in fall 2021." - Prof. Dr. Nina Gantert (TUM), Mentorin von Dominik Schmid
"Claudia Stadlmayr zeigte bereits in ihrer TopMath-Bachelorarbeit 'Deformations and Resolutions of Rational Double Points' ein außerordentlich tiefes Verständnis für algebraische Geometrie. Inzwischen liegen von ihr bereits zwei Preprints mit eigenen Resultaten vor: 'Weak del Pezzo surfaces with global vector fields' (50 Seiten, gemeinsam mit Gebhard Martin) und 'Which rational double points occur on del Pezzo surfaces?' (20 Seiten). Beide Arbeiten haben bereits für Aufsehen in der Fachwelt und zu weltweiten Votragseinladungen geführt. Ihre Arbeit greift zentrale Fragestellungen des Minimal Model Programms (oder Mori-Programms) in Dimension 2 auf und beantwortet sie vollständig. In der reinen Mathematik ist dies in diesem frühen Karrierestadium höchst bemerkenswert und außergewöhnlich." - Prof. Dr. Christian Liedtke (TUM), Mentor von Claudia Stadlmayr