Für ihre herausragenden Leistungen zeichnete das TopMath-Board Chris ShuYu Dong (Forschungsgruppe Decision Sciences & Systems/ TUM) und Helge Tilmann Frerichs (Forschungsgruppe Differentialgeometrie der Universität Augsburg) ex aequo mit dem TopMath Award 2024 aus.
Der TopMath Award ist eine Auszeichnung für Promovierende des Programms, die sich durch herausragende Forschungsleistungen besonders hervorgetan haben. Er wird einmal jährlich verliehen. Nach einem Vorschlag ihrer Mentorin, ihres Mentors oder des Fachstudienberaters werden die Kandidat*innen zum Anfang des Wintersemesters zu einer Eigenbewerbung aufgefordert. Jeweils in seiner letzten Jahressitzung bestimmt das TopMath-Board nach ausführlicher Beratung den*die Preisträger*in. Der TopMath Award ist mit 500 € dotiert und wird im feierlichen Rahmen der Absolventenfeier der School of CIT der TUM vergeben.
Preisträger des TopMath Award 2024 sind ex aequo Chris Dong (Forschungsgruppe Decision Sciences & Systems) und Helge Tilmann Frerichs (Forschungsgruppe Differentialgeometrie der Universität Augsburg).
Wir gratulieren den Preisträgern herzlich und wünschen ihnen weiterhin viel Erfolg bei der Verfolgung ihrer mathematischen Ziele!
Chris Dong: Social choice theory
Text: Chris Dong
Social choice theory untersucht, wie individuelle Präferenzen zu kollektiven Entscheidungen zusammengeführt werden können. Um dem Ergebnis einer demokratischer Wahl legitimität zu verleihen, ist eine ausreichende Beteiligung durch die Wählerschaft notwendig. Die Wahlregeln sollten daher immer einen Anreiz für potenzielle Wählerinnen bieten, ihre Stimmen abzugeben - unter keinen Umständen sollte eine Stimmenthaltung, ceteris paribus, zu einem besseren Ergebnis für eine Wählerin führen als eine ehrliche Teilnahme. Dieses Axiom/Prinzip wird als Partizipation bezeichnet.
Moulin (1988) wies nach, dass Partizipation nicht kompatibel ist mit einer anderen vernünftigen Eigenschaft für Wahlen, bei denen es nur eine Gewinnerin gibt (z. B. bei Präsidentschaftswahlen). Im Gegensatz dazu haben zustimmungsbasierte Komittee-Wahlen (ABC-Wahlen) in den letzten zehn Jahren erheblich an Aufmerksamkeit gewonnen. Hier wird ein Kommittee fester Größe (z. B. ein parlamentarisches Gremium) zusammengestellt, und jede Wählerin kreuz alle Kandidatinnen an, die sie für gut befindet.
Meine Forschung untersucht Partizipation bei ABC-Wahlen und macht folgende Beiträge:
* Wir zeigen, dass ABC-Scoring Regeln eine starke Form von Partizipation erfüllen. Selbst die koordinierte Enthaltung von Wählergruppen kann nicht dazu führen, dass alle Mitglieder schwach profitieren und mindestens ein Wähler strikt profitiert.
* Während viele ABC-Scoring Regeln nicht effizient implementiertbar sind, werden häufig sequentielle Regeln verwendet, die das Komittee Kandidatin für Kandidatin zusammenstellen. Wir formulieren eine axiomatische Inkompatibilität für diese sequentiellen Regeln. Dafür konstruieren wir Wahlszenarien, in denen sequentielle Regeln Partizipation stark verletzen, und identifizieren Eigenschaften, die für das unerwünschte Verhalten verantwortlich sind.
* Wir zeigen, dass unter bestimmten Annahmen strategische Enthaltung für viele häufig untersuchte sequentielle Regeln nicht vorteilhaft oder nicht effizient berechenbar ist.
Durch diese Arbeit vereinheitlichen und erweitern meine Co-Autoren und ich frühere Studien über die Robustheit von ABC-Wahlregeln, einschließlich der Erkenntnisse von Janson (2016), Sánchez-Fernández und Fisteus (2019) und Lackner und Skowron (2023).
Helge Frerichs: Skalarkrümmung und nicht-kompakte Ränder
Text: Helge Tilmann Frerichs
Grundsätzlich beschäftige ich mich in meiner Forschung mit einer bestimmten Klasse gekrümmter Räume, genauer mit berandeten differenzierbaren Mannigfaltigkeiten und ihren möglichen riemannschen Metriken. Im Einzelnen untersuche ich das Wechselspiel zwischen der sogenannten Skalarkrümmung einer Mannigfaltigkeit und der mittleren Krümmung ihres Randes.
Die Skalarkrümmungsgeometrie ist heute ein eigenständiges Forschungsgebiet innerhalb der Differentialgeometrie. Es bestehen jedoch enge Beziehungen zu anderen Disziplinen in der Mathematik – vor allem zur Topologie – und zur mathematischen Physik. Hier sind Anwendungen in der allgemeinen Relativitätstheorie von Interesse.
Im Mittelpunkt meiner eigenen Forschung stehen Mannigfaltigkeiten mit nicht-kompakten Rändern, die bisher wenig untersucht sind. Auf einigen dieser Mannigfaltigkeiten konnte ich Nicht-Existenzresultate für riemannsche Metriken mit (uniform) positiver Skalarkrümmung und mittel-konvexem Rand – das heißt mit nicht-negativer mittlerer Krümmung – beweisen. Als zentrales Mittel kommt dabei ein von mir weiterentwickeltes Deformationsprinzip für riemannsche Metriken zum Einsatz, mit dem die Geometrie des Randes unter Einhaltung unterer Skalarkrümmungsschranken adaptiert werden kann.
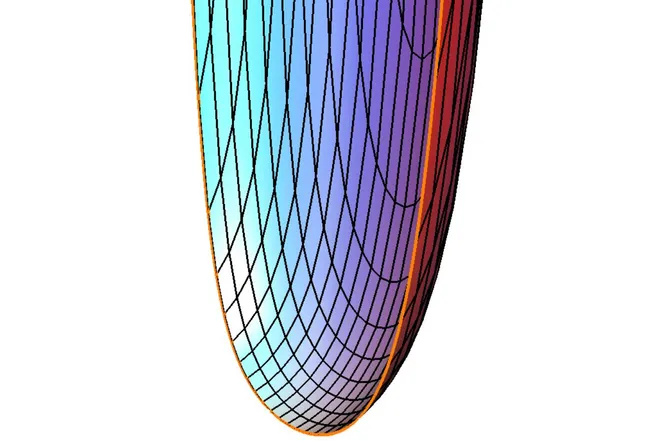
Um einen Eindruck von den genannten geometrischen Eigenschaften zu bekommen, ist oben eine Halbebene mit positiver, aber nicht uniform positiver Skalarkrümmung und mittel-konvexem Rand dargestellt. Ein Nicht-Existenzresultat für Halbebenen erhält man durch die Forderung einer uniformen Schranke an die Skalarkrümmung.
Link zur Arbeit: Scalar curvature deformations with non-compact boundaries
Ein breiteres mathematisch interessiertes Publikum verweise ich auf meinen Übersichtsartikel, der 2024 in den Mitteilungen der DMV erschienen ist.
Link zum Artikel: Skalarkrümmung und nicht-kompakte Ränder
Stimmen zu den Preisträgern und ihren Leistungen
„Die Forschungsarbeit von Chris Dong gehört zum Bereich der computergestützten Sozialwahltheorie, einem interdisziplinären Studienbereich an der Schnittstelle von Mathematik, Informatik und Wirtschaft. Die Ergebnisse, die Chris und seine Mitautoren erzielt haben, verbessern unser Verständnis von zustimmungsbasierten ABC-Ausschusswahlen erheblich. Eine ABC-Wahlregel bildet die Menge der zugelassenen Kandidaten der Wähler auf ein Komitee mit fester Größe ab. Chris' Arbeit mit Martin Bullinger, Patrick Lederer und Clara Mehler ist die erste, die explizit die Anreize zur Teilnahme in diesem Umfeld untersucht. In anderen Arbeiten entwickelte Chris ansprechende axiomatische Charakterisierungen von punktebasierten Wahlregeln. Die Proceedings der Informatikkonferenzen, auf denen Chris seine Ergebnisse veröffentlicht hat, werden von Fachkollegen begutachtet und sind sehr kompetitiv. Sie umfassen mehrere Begutachtungs- und Widerlegungsrunden, und die Annahmequote liegt in der Regel unter 25 %. Chris hatte das seltene Vergnügen, zwei Vorträge auf der AAAI 2024 zu halten, einer der führenden internationalen Konferenzen im Bereich der künstlichen Intelligenz, die mehr als 5000 Teilnehmer anzieht.“ Prof. Dr. Felix Brandt (TUM), Mentor von Chris Dong
„Helge Frerichs beweist neue Flexibilitätsresultate für riemannsche Mannigfaltigkeiten mit unteren Skalarkrümmungsschranken im Inneren und unteren mittleren Krümmungsschranken am Rand. Als Novum behandelt er auch nicht kompakte Ränder. Hier kommen subtile topologische und global-geometrische Eigenschaften wie der Quasi-Isometrietyp der zugrundeliegenden Mannigfaltigkeit ins Spiel. Als Anwendung beweist Frerichs neue Klassifikationssätze in der Skalarkrümmungsgeometrie. Diese hat in letzter Zeit viel Aufmerksamkeit auf sich gezogen, insbesondere durch den enzyklopädischen Übersichtsartikel Four Lectures on Scalar Curvature von Misha Gromov aus dem Jahr 2021.
Weitere differentialgeometrische und spektralgeometrische Implikationen seiner bisherigen Ergebnisse sind Gegenstand des Promotionsvorhabens von Helge Frerichs.
Seine Masterarbeit wurde auf der DMV-Studierendenkonferenz StuKon im Sommer 2023 mit einem Hauptpreis ausgezeichnet, woraufhin er einen längeren Forschungsaufenthalt am MPI MiS Leipzig verbrachte.“ Prof. Dr. Bernhard Hanke (Universität Augsburg), Mentor von Helge Frerichs