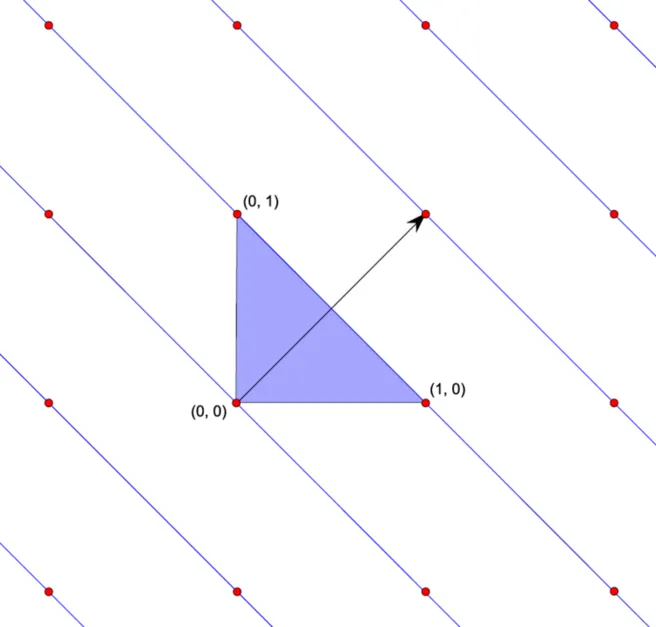
Lower bounds on the flatness constant
When trying to fit a convex set between the points of a lattice, it becomes apparent that such a set always has to be somewhat flat. The lattice-width of a convex body is a quantity that measures this flatness with regard to the lattice that constricts the body. The well-known Flatness Theorem states that the lattice-width of a d-dimensional lattice-free convex set is bounded from above by a constant Flt(d) that only depends on the dimension d. While there have been lots of results concerned with upper bounds to this constant, only few techniques are known to obtain lower bounds and so far, the best known lower bound was Flt(d) ≥ 1.138d. In this talk, we will discuss a construction of a series of simplices that yields the lower bound Flt(d) ≥ 2d - O(sqrt(d)).
https://arxiv.org/abs/2111.08483
Der Vortrag findet in Raum FMI 02.06.011 statt; zusätzlich können sie ihn online verfolgen.
TopMath-Talks
Im Rahmen der TopMath-Talks stellen Studierende und Promovierende des TopMath-Programms Teile ihrer Forschung vor. Sie geben einen verständlichen Einblick in ihr Interessensgebiet und ermöglichen es so Studierenden und Mitarbeitern, ihre mathematische Allgemeinbildung zu erweitern. Die Talks sind öffentlich und dauern ungefähr eine Stunde mit anschließender Diskussion. Jede*r ist willkommen.