For their outstanding achievements, the TopMath Board honoured Chris ShuYu Dong (Decision Sciences & Systems research group) and Helge Tilmann Frerichs (Differential Geometry research group at the University of Augsburg) ex aequo with the TopMath Award 2024.
The TopMath Award is an award for doctoral candidates in the programme who have distinguished themselves through outstanding research achievements. It is awarded once a year. Following a proposal from their mentor or academic advisor, candidates are invited to submit their own application at the beginning of the winter semester. At its final meeting of the year, the TopMath Board selects the winner after extensive consultation. The TopMath Award is endowed with €500 and is presented at the TUM School of CIT's graduation ceremony.
The winners of the TopMath Award 2024 are ex aequo Chris Dong (Decision Sciences & Systems research group) and Helge Tilmann Frerichs (Differential Geometry research group at the University of Augsburg).
We congratulate the award winners and wish them continued success in the pursuit of their mathematical goals!
Chris Dong: Social choice theory
Text: Chris Dong
Social choice theory studies how individual preferences can be aggregated into collective decisions. A key aspect of democratic elections is ensuring sufficient participation to justify the outcome of a vote. Voting rules should, therefore, always incentivize potential voters to cast their ballots—under no circumstances should abstaining result in a better outcome for a voter than truthfully participating. This principle is known as participation.
Moulin (1988) demonstrated that participation is inherently at odds with another reasonable property in the standard voting setting, where the outcome is a single winner (e.g., in presidential elections). In contrast, approval-based committee (ABC) voting, which seeks to assemble a fixed-size committee (e.g., a parliamentary body) given approval ballots of the voters, has gained significant attention over the past decade.
My research investigates participation in ABC voting, with the following key contributions:
* We show that ABC scoring rules satisfy a strong form of participation. Even coordinated abstention by groups of voters cannot result in all members weakly benefiting, with at least one voter strictly benefiting.
* While many ABC scoring rules are computationally intractable, sequential "greedy" rules are commonly used that assemble the committee candidate by candidate. We present an axiomatic impossibility for these sequential rules, identifying scenarios where they fail participation severely and uncovering the underlying properties that lead to these failures.
* We demonstrate that under certain restricted assumptions, strategic abstention is either impossible or computationally intractable for many commonly studied sequential rules.
Through this work, my co-authors and I unify and extend previous studies on the robustness of ABC voting rules, including insights from Janson (2016), Sánchez-Fernández and Fisteus (2019), and Lackner and Skowron (2023).
Helge Frerichs: Scalar curvature and non-compact boundaries
Text: Helge Tilmann Frerichs
The subject of my research is a certain class of curved spaces, namely differentiable manifolds with boundary and their possible riemannian metrics. Specifically, I study the interplay between the so-called scalar curvature of a manifold and the mean curvature of its boundary.
Today, scalar curvature geometry is an independent field of research within differential geometry. However, there are close links with other disciplines in mathematics – especially topology – and mathematical physics. Applications to general relativity are of particular interest.
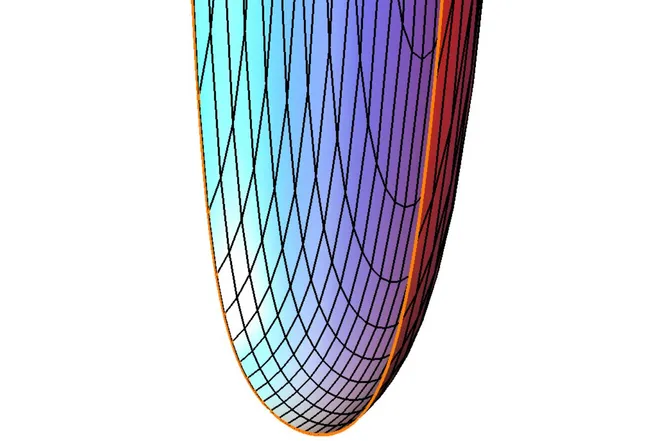
My own research focuses on manifolds with non-compact boundaries, which have been little studied so far. On some of these manifolds I was able to prove non-existence results for riemannian metrics with (uniformly) positive scalar curvature and mean convex boundary, i.e. with non-negative mean curvature. This can be done by applying a deformation principle for riemannian metrics that I have improved, which is used to adapt the geometry of the boundary while preserving lower scalar curvature bounds.
To get an idea of the geometric properties mentioned, the figure above shows a half-plane with positive, but not uniformly positive scalar curvature and mean convex boundary. A non-existence result for half-planes is obtained by requiring a uniform bound on the scalar curvature.
Link to the paper: Scalar curvature deformations with non-compact boundaries
For a wider audience, I refer to my article in the Mitteilungen der DMV which appeared in 2024.
Link to the article: Skalarkrümmung und nicht-kompakte Ränder
Acknowledgement of the prize winners and their achievements
“Chris Dong’s research belongs to the area of computational social choice, an interdisciplinary field of study at the intersection of mathematics, computer science, and economics. The results that Chris and his coauthors obtained significantly improve our understanding of approval-based committee ABC elections. An ABC voting rule maps the voters’ sets of approved candidates to a committee of fixed size. Chris' paper with Martin Bullinger, Patrick Lederer, and Clara Mehler is the first to explicitly study participation incentives in this setting. In other work, Chris developed appealing axiomatic characterizations of score-based voting rules. The proceedings of the computer science conferences where Chris published his results are peer-reviewed and highly competitive. They involve several rounds of reviewing and rebuttals, and the acceptance rates are typically below 25%. Chris had the rare pleasure of presenting two papers at AAAI 2024, one of the leading international conferences in the area of artificial intelligence, attracting more than 5000 attendees.” Prof. Dr. Felix Brandt (TUM), Mentor of Chris Dong
“Helge Frerichs proves new flexibility results for Riemannian manifolds with lower scalar curvature bounds in the interior and lower mean curvature bounds along the boundary. As a novelty, he also treats non-compact boundaries. Here, subtle topological and global-geometric properties such as the quasi-isometry type of the underlying manifold come into play. As an application, Frerichs proves new classification theorems in scalar curvature geometry. This has attracted a lot of attention recently, in particular due to the encyclopedic survey article Four Lectures on Scalar Curvature by Misha Gromov from 2021.
Further differential geometric and spectral geometric implications of his previous results are the subject of Helge Frerichs' doctoral dissertation project.
His master's thesis was awarded a main prize at the DMV Student Conference StuKon in the summer of 2023, whereupon he spent an extended research stay at the MPI MiS Leipzig.” Prof. Dr. Bernhard Hanke (University of Augsburg), mentor of Helge Frerichs