Geometric complexes and their topological properties
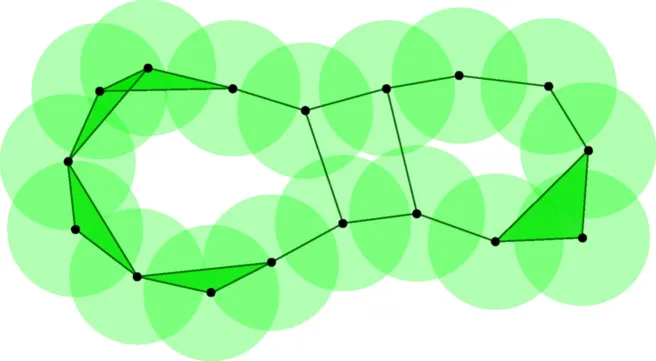
Geometric complexes are the main tool in topological data analysis to replace a point cloud with a combinatorial model that is suitable for computations. In this talk, I will focus on two such complexes, namely the Čech complex, which arises as the nerve of a collection of closed balls, and the Vietoris-Rips complex, which arises directly from the metric structure of the underlying space.
After explaining these constructions, I will survey certain aspects of their long history, which dates back to the early days of algebraic topology, mention the original application to geometric group theory, and discuss their prominent use nowadays in the context of persistent homology. The topology and geometry of the underlying space strongly influences the homotopy type of the Čech and the Vietoris-Rips complex. The main goal of this talk is to showcase this phenomenon by presenting selected results, such as the nerve theorem, Latschev's theorem on the reconstruction of Riemannian manifolds from a finite point sample, and Rips' contractibility lemma for Gromov delta-hyperbolic metric spaces. For the latter I will point out some interesting connections to the study of COVID-19 genetic evolution data and the outstanding performance on genetic distances of Ripser, which is the current state of the art software to compute Vietoris-Rips persistent homology.
TopMath Talks
As part of the TopMath talks, TopMath students and doctoral students present parts of their research. They provide an understandable insight into their current area of interest, enabling students and staff to broaden their mathematical background knowledge. The talks are open to the public and last about an hour, followed by discussion. You are cordially invited!